41 KMP子串查找算法

KMP子串查找算法(一)

问题如何在目标字符串S中，查找是否存在子串P?

朴素解法

int sub_str_index(const char *s, const char *p) {
    int ret = -1;
    int sl = strlen(s);
    int pl = strlen(p);
    int len = sl - pl;
    for (int i = 0; (ret < 0) && (i <= len); i++) {
        bool equal = true;
        for (int j = 0; equal && (j < pl); j++)
            equal = equal && (s[i + j] == p[j]);
        ret = (equal ? i : -1);
    }
    return ret;
}

朴素解法的一个优化线索

因为，p_a != p_b,且p_b == s_b; 所以，p_a != s_b; 结论，子串p右移1位比较，没有意义。
示例
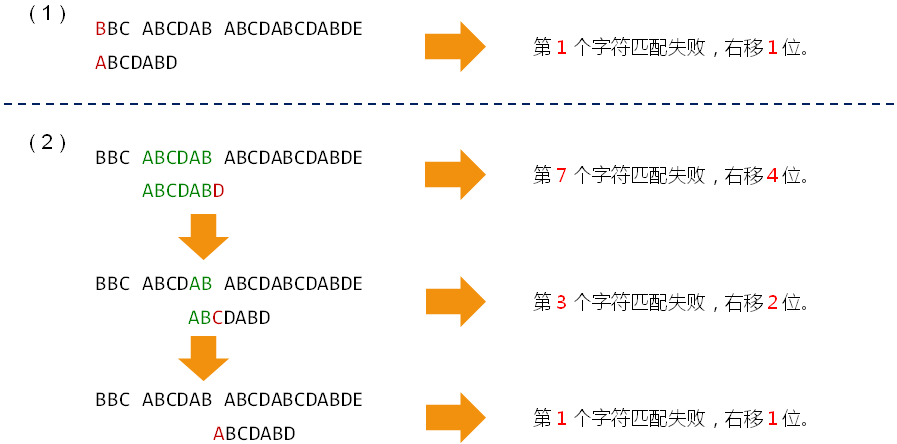
伟大的发现
- 匹配失败时的右移位数与子串本身相关，与目标串无关
- 移动位数 = 已匹配的字数-对应的部分匹配值
- 任意子串都存在一个唯一的部分匹配表
部分匹配表示例

Partial Matched Table

1 2 3 4 5 6 7
A B C D A B D
0 0 0 0 1 2 0

用法：

第7位匹配失败→前6位匹配成功→查表PMT[6]→右移位数6-PMT[6]=6-2=4
问题部分匹配表是怎么得到的？
前缀
- 除了最后一个字符以外，一个字符串的全部头部组合
后缀
- 除了第一个字符以外，一个字符串的全部尾部组合
部分匹配值
- 前缀和后缀最长共有元素的长度
示例：ABCDABD

1	2	3	4	5	6	7
A	B	C	D	A	B	D
0	0	0	0	1	2	0

-	字符	前缀	后缀	交集	匹配值
1	A	空	空	空	0
2	AB	A	B	空	0
3	ABC	A,AB	BC,C	空	0
4	ABCD	A,AB,ABC	BCD,CD,D	空	0
5	ABCDA	A,AB,ABC,ABCD	BCDA,CDA,DA,A	A	1
6	ABCDAB	A,AB,ABC,ABCD,ABCDA	BCDAB,CDAB,DAB,AB,B	AB	2
7	ABCDABD	A,AB,ABC,ABCD,ABCDA,ABCDAB	BCDABD,CDABD,DABD,ABD,BD,D	空	0

问题怎么编程产生部分匹配表？
实现关键
- PMT[1] = 0(下标为0的元素匹配值为0)
- 从2个字符开始递推(从下标为1的字符开始递推)
- 假设PMT[n]=PMT[n-1]+1(最长共有元素的长度)
- 当假设不成立，PMT[n]在PMT[n-1]的基础上减小

编程实验(一)

部分匹配表的递推与实现

size_t* make_pmt(const char *p){
    auto len = strlen(p);
    auto *ret = reinterpret_cast<size_t*>(malloc(sizeof (size_t)*len));
    if(ret!=nullptr){
       size_t ll=0;
        ret[0] = 0;
        for (size_t i=1;i<len;i++) {
            while ((p[ll]!=p[i])&&(ll>0)){
                ll = ret[ll-1];
            }
            if(p[ll]==p[i]) ll++;
            ret[i]=ll;
        }
    }
    return ret;
}

KMP子串查找算法(二)

部分匹配表的使用(KMP算法)

下标j处匹配失败→前j位匹配成功→查表PMT[j-1]→右移位数j-PMT[j-1]

因为，s[i]!=p[j]

所以，查表，LL=PMT[j-1]

于是，右移，i的值不变，j的值改变，j=j-(j-LL)=LL=PMT[j-1];

编程实验(二)

KMP子串查找算法的实现

int kmp(const char*s,const char*p){
    int ret = -1;
    auto sl = strlen(s);
    auto pl = strlen(p);
    auto pmt = make_pmt(p);
    if((pmt!=nullptr)&&(0<pl)&&(pl<=sl)){
        for (size_t i=0,j=0;i<sl;i++) {
            while ((j>0)&&(s[i]!=p[j])) {
                j=pmt[j-1];
            }
            if(s[i]==p[j]) j++;
            if(j==pl) ret = static_cast<int>(i+1-pl);
        }
    }
    free(pmt);
    return ret;
}

小结

部分匹配表是提高子串查找效率的关键
部分匹配值定义为前缀和后缀最长共有元素的长度
可以用递推的方法产生部分匹配表
KMP利用部分匹配表与子串移动位数的关系提高查找效率

42 KMP算法的应用

KMP算法的应用

思考如何在目标字符串中查找是否存在指定的子串？
```
String s = "Hello World!";
int pos = s.indexof("ll");    //2
```

字符串类中的新功能

成员函数	功能描述
indexOf(s)	查找子串s在字符串中的位置
remove(s)	将字符串中的子串s删除
operator-(s)	定义字符串减法
replace(s,t)	将字符串中的子串s替换为t
sub(i,len)	从字符串中创建子串

子串查找(KMP算法的直接应用)
- int indexOf(const char *s)const
- int indexOf(const String &s)const
在字符串中将指定的子串删除
- String& remove(const char *s)
- String& remove(const String &s)
1. 根据KMP在目标字符串中查找子串的位置
2. 通过子串位置和子串长度进行删除
字符串的减法操作定义(operator-)
- 使用remove实现字符串间的减法操作
- 字符串自身不被修改
- 返回产生的新串
```
String s1 = "abcde";
String s2 = s1 - "bcd";
cout << s1.str()<<endl;    //abcde
cout << s2.str()<<endl;    //ae
```
字符串中的子串替换
- String& replace(const char *t,const char *s)
- String& replace(const String &t,const char *s)
- String& replace(const char *t,const String &s)
- String& replace(const String &t,const String &s)
从字符串中创建子串
- String sub(int i,int len)const
- 以i为起点提取长度为len的子串
- 子串提取不会改变字符串本身的状态
```
String s1 = "abcde";
String s2 = s1.sub(1,3);
cout << s1.str()<<endl;    //abcde
cout << s2.str()<<endl;    //bcd
```

编程实验

新成员函数的实现

//KylinString.h
#ifndef KYLINSTRING_H
#define KYLINSTRING_H

#include "Object.h"

namespace KylinLib {

class String
{
//...
    int indexOf(const char *s)const;
    int indexOf(const String &s)const;

    String& remove(size_t index,size_t length);
    String& remove(const char *s);
    String& remove(const String &s);

    String& replace(const char *t,const char *s);
    String& replace(const String &t,const char *s);
    String& replace(const char *t,const  String &s);
    String& replace(const String &t,const  String &s);

    String sub(size_t index,size_t length)const;

    String& operator-= (const char *str);
    String& operator-= (const String &str);

    String operator-(const char *str) const;
    String operator-(const String &str) const;

protected:
    static size_t* make_pmt(const char *p);
    static int kmp(const char *s,const char *p);
	//...
};
}
#endif // KYLINSTRING_H

//KylinString.cpp
#include "KylinString.h"
#include "Exception.h"
#include <stdlib.h>
#include <string.h>

namespace KylinLib {


int String::indexOf(const char *s) const
{
    return kmp(m_str,s);
}

int String::indexOf(const String &s) const
{
    return indexOf(s.m_str);
}

String &String::remove(size_t index, size_t length)
{
    if(index>=m_length)
        THROW_EXCEPTION(InvalidParameterException,"Index is invalid...");
    size_t begin = index+length;
    for (;begin<m_length;begin++,index++) {
        m_str[index]=m_str[begin];
    }
    m_str[index]='\0';
    m_length = index;
    return *this;
}

String &String::remove(const char *s)
{
    auto pos = indexOf(s);
    if(pos>=0) remove(static_cast<size_t>(pos),strlen(s));
    return *this;
}

String &String::remove(const String &s)
{
    return remove(s.m_str);
}

String &String::replace(const char *t, const char *s)
{
    auto pos = indexOf(t);
    if(pos>0){
        remove(t);
        insert(static_cast<size_t>(pos),s);
    }
    return *this;
}

String &String::replace(const String &t, const char *s)
{
    return replace(t.m_str,s);
}

String &String::replace(const char *t, const String &s)
{
    return replace(t,s.m_str);
}

String &String::replace(const String &t, const String &s)
{
    return replace(t.m_str,s.m_str);
}

String String::sub(size_t index, size_t length) const
{
    if(index>=m_length)
        THROW_EXCEPTION(InvalidParameterException,"Parameter index is invalid...");
    if((index+length)>=m_length) length = m_length-index;

    auto str = reinterpret_cast<char*>(malloc(length+1));
    strcpy(str,m_str+index);
    str[length]='\0';
    String ret(str);
    free(str);
    return ret;
}

String &String::operator-=(const char *str)
{
    return remove(str);
}

String &String::operator-=(const String &str)
{
    return remove(str);
}

String String::operator-(const char *str)const
{
    String ret(*this);
    return (ret-=str);
}

String String::operator-(const String &str)const
{
    String ret(*this);
    return (ret-=str);
}

size_t *String::make_pmt(const char *p)
{
    auto len = strlen(p);
    auto *ret = reinterpret_cast<size_t*>(malloc(sizeof (size_t)*len));
    if(ret!=nullptr){
       size_t ll=0;
        ret[0] = 0;
        for (size_t i=1;i<len;i++) {
            while ((p[ll]!=p[i])&&(ll>0)){
                ll = ret[ll-1];
            }
            if(p[ll]==p[i]) ll++;
            ret[i]=ll;
        }
    }
    return ret;
}

int String::kmp(const char *s, const char *p)
{
    int ret = -1;
    auto sl = strlen(s);
    auto pl = strlen(p);
    auto pmt = make_pmt(p);
    if((pmt!=nullptr)&&(0<pl)&&(pl<=sl)){
        for (size_t i=0,j=0;i<sl;i++) {
            while ((j>0)&&(s[i]!=p[j])) {
                j=pmt[j-1];
            }
            if(s[i]==p[j]) j++;
            if(j==pl) ret = static_cast<int>(i+1-pl);
        }
    }
    free(pmt);
    return ret;
}


}

小结

字符串类是工程开发中必不可少的组件
字符串中应该包含常用字符串操作函数
增:insert,operator+,...
删:remove,operator-,...
查:indexOf,...
改:replace,...

KMP子串查找算法(一)​

编程实验(一)​

KMP子串查找算法(二)​

编程实验(二)​

小结​

42 KMP算法的应用

KMP算法的应用​

编程实验​

小结​

KMP子串查找算法(一)

编程实验(一)

KMP子串查找算法(二)

编程实验(二)

小结

KMP算法的应用

编程实验

小结